|
Reliability Growth Modeling |
|
|
|
|
Reliability Growth Modeling |
|
|
Reliability Growth Modeling
|
Reliability Growth Modeling |
|
|
|
|
Reliability Growth Modeling |
|
|
Reliability Growth Modeling
RAM Commander’s reliability growth module is the Duane method as described in MIL-STD-1635. In this model, the tested mean time between failure (MTBF) is proportional to Tα where T is the cumulative operating test time and α is the growth rate index. On a log-log plot, the growth regression line is linear with slope α.
The cumulative mean time before failure (MTBFc) is normally measured during testing and then divided by (1 - α) to convert it to the current instantaneous mean time before failure MTBFi. MTBFi is then plotted parallel to the MTBFc at an offset of 1/(1 - α). The test time at which this line reaches the required MTBF is the expected duration of the reliability growth test.
RAM Commander uses Bootstrap, a new statistical technology that enables the user to calculate accurate confidence intervals for the main parameters of the Duane model by obtaining a large number of samples. Details of this method have been published in the paper “Bootstrap Technology for RAM Analysis”, Z. Bluvband and L. Peshes, Proceedings of the Symposium on New Directions in Military Reliability, Availability and Maintainability (RAM) Analysis, Maryland, USA, 1993.
Derivation of Model Equations
According to the Duane formulation:
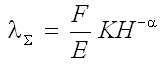
where:
λΣ |
cumulative failure rate |
H |
total test hours |
F |
failure during H hours |
K |
condition-dependent coefficient |
α |
growth rate |
The original mathematical model was expressed in terms of cumulative failure rate. However, since equipment reliability is generally expressed in terms of MTBF, the following expression is more frequently used:
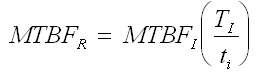
where:
MTBFR |
required MTBF |
MTBFI |
initial MTBF |
ti |
time at which initial data point is plotted (preconditioning time) |
Ti |
time at which the instantaneous MTBF of the equipment under test will reach the required MTBF |
Differentiating the equation with respect to time, we receive
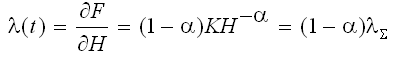
Thus, the current instantaneous failure rate is (1 – α) times the cumulative failure. That is, the instantaneous MTBF is 1/(1 – α) times the cumulative MTBF.
The instantaneous MTBF may be interpreted as the MTBF that the equipment under test would exhibit if we stopped the reliability growth and continued testing. Thus, on a logarithmic plot, instantaneous or current-status curves are straight lines displaced a fixed distance from the cumulative plot by a factor of (1 – α).
The cumulative MTBF (MTBFc) is normally measured during testing and then converted to the instantaneous (or current) MTBF (MTBFi) by dividing by (1 – α), that is:
.
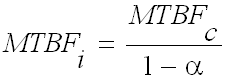